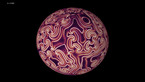
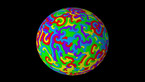
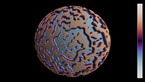
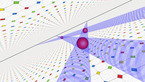
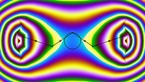
Waves with cubic symmetry on the sphere, 2d projection
film
Lizenz
Autoren
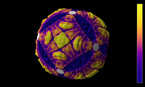
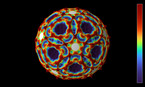
Solution of the wave equation on a sphere. Reflecting obstacles have been placed around the vertices of a cube. The initial state is a set of circular waves of alternating sign, concentrated at the centers of the faces of the cube and on the centers of its edges. The video shows an equirectangular projection.
The simulation shows a solution of the wave equation on a sphere, obtained by a finite difference scheme. There are Dirichlet boundary conditions on a set of discs of constant radius placed on the vertices of a cube. The initial state is a set of circular waves concentrated near the centers of the faces of the cube, which form a regular octahedron, and on the centers of the cube’s edges. The amplitudes have alternating signs (that is, there are phase shifts ov pi between neighboring sources).
The point of view rotates around the sphere in the course of the simulation. Part 1 shows the wave height, while part 2 shows the energy flux, slightly averaged over time.