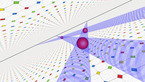
Suites d'intersections sur le Pentagone Double
films
Licence
Crédits
En utilisant les couleurs et les mouvements, la vidéo illustre ce que j’ai prouvé dans ma thèse de doctorat. Elle explique ce qu’est une surface de translation et quel est le théorème démontré à leur sujet.
Le but de cette vidéo est d’expliquer, à travers la danse, les résultats de ma thèse de doctorat. Mon objectif second est de montrer ce que la recherche mathématique signifie vraiment (la plupart des gens pensent qu’il ne s’agit que de regarder des formules dans des livres).
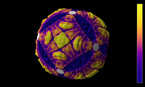
La danseuse (Libby) nous montre au début de la vidéo comment deux pentagones peuvent être collés et former une surface. Il s’agit de l’idée clef de cette vidéo, l’explication de la science sans parole, juste par la danse. Elle est facilement compréhensible et reste en mémoire. C’est ma partie préférée!
D’accord. Revenons à nos moutons. Imaginez que vous marchez sur une ligne droite sur un bagel (petit pain avec un trou). Vous passerez peut-être directement par le trou avant de retourner à l’endroit où vous avez commencé. Ou sinon vous ferez peut-être le tour par l’extérieur (comme si vous suiviez l’équateur) et retournerez là où vous étiez. Ou peut être marcherez-vous sur un chemin en spirale (toujours une ligne droite), à travers le trou et autour du bagel un certain nombre de fois avant de retourner là où vous avez commencé.
Dans la partie suivante de la vidéo, Libby danse à travers le pentagone en ligne droite. C’est exactement ce que j’essayais d’expliquer en parlant de chemin en spirale sur le bagel: elle danse en ligne droite et continue sur la surface plusieurs fois (huit fois car il y a huit segments de droites sur les pentagones) avant de retourner là où elle avait commencé et de répéter le parcours.
Quand Libby danse en ligne droite sur les pentagones, elle traverse les côtés colorés de ceux-ci. On prête attention à ces côtés traversés, et nous pouvons garder leur trace en utilisant un personnage dont la couleur du tee-shirt est celle du côté. Cela créé une suite de couleurs périodique qui se répète au bout de huit fois.
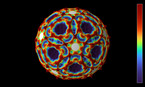
Mes recherches sont basées sur les changements des suites de couleurs lorsque la surface du pentagone est modifiée. On «déforme, on coupe et on réassemble ces pentagones», voilà ce qui est montré dans le vidéo. Les huit lignes d’origine des pentagones prennent une forme différente: quatre lignes à l’évidence. Quand Libby danse sur ces quatre lignes, elle réalise des spirales différentes mais aussi plus petites sur le bagel. Elle traverse les côtés colorés, ce qui nous donne une nouvelle suite de personnages aux tee-shirts colorés.
La problématique de ma thèse est: quelle est la différence entre la suite de couleurs de longueur 8 et celle de longueur 4?
La réponse: Chaque personnage vérifie si il/elle est entouré-e par la même couleur des deux côtés. Si oui, il/elle reste en ligne (garde son chapeau), sinon, il/elle doit partir (retire son chapeau).
Voici mon théorème: le fait de déformer et de réassembler les pentagones est équivalent au fait de voir si les couleurs sont les mêmes des deux côtés.
Je ne suis pas la première personne à avoir prouvé un théorème de ce genre. John Smillie et Corinna Ulcigrai ont étudié les surfaces octogonales régulières, ce qui est similaire au pentagone double excepté le fait qu’on identifie les côtés opposés parallèles (de la même couleur) de l’octogone. Ils ont prouvé qu’en «déformant, coupant et en réassemblant l’octogone, l’effet sur la suite des couleurs est de garder seulement les éléments ayant la même couleur des deux côtés. Ma contribution a été de montrer que ces méthodes s’appliquent aussi aux surfaces en pentagones doubles.
Si cela vous intéresse, plus de détails figurent sur mon article dont la vidéo constitue le résumé: http://www. math. northwestern.edu/~diana/math/VeechPolygons.pdf. L’introduction de cet article est très accessible et contient beaucoup d’images. En référence, vous pourrez trouver les articles de Smillie et de Ulcigrai, dont l’introduction est aussi accessible à tous. Les côtés de ces polygones y sont identifiés par des lettres et non plus par des couleurs.