이 비디오의 목적은 춤을 통하여 제 박사학위 논문을 설명하는 것입니다. 또 한가지 바램이 있다면, 이 비디오가 “수학 연구”란 무엇인지 여러분들에게 보여드릴 수 있으면 좋겠습니다.

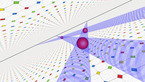
첫 1분 동안, 무용수 리비(Libby)는 두개의 오각형이 어떻게 표면을 만들기 위해 합쳐지는지 보여줍니다. 이것이 지루한 설명 없이 춤을 통해 수학을 설명하고자 하는 이 영상의 핵심입니다. 여러분들이 직접 이해하시고 기억하신다면 대단히 기쁘겠습니다.

잠시 영상을 멈추고, 여러분들이 3차원 도넛 위를 직선으로 걷는다고 상상해 보십시오. 어쩌면 여러분은 도넛의 구멍을 직접 통과하여 출발점으로 돌아올지도 모릅니다. 어쩌면 어려분은 마치 지구의 적도처럼 도넛의 바깥면을 따라 걸어 출발점으로 돌아올지도 모릅니다. 아니면 도넛의 중심을 향해 사선으로 걸으며, 몇 바퀴를 돈 후 다시 출발점으로 돌아올지도 모릅니다.

리비가 오각형들 사이를 직선으로 지나갈때, 그녀는 오각형의 변들을 통과하며 다닙니다. 우리는 그녀가 무슨 색의 변을 통과하는지 Math Hatter를 통해 기록합니다. 이 결과 우리는 연속하는 색들의 기록을 얻게됩니다. 

간단히 말해, 제 박사논문은 우리가 오각형으로 만들어진 표면을 변화시킬 시에 이 연속되는 색들의 기록이 어떻게 바뀌는지 알아보는 것 이였습니다. 이 비디오에서 우리는 오각형 표면을 변화시켜 기존의 8개의 선을 4개의 선으로 바꿨습니다. 리비가 4개의 선을 따라 춤을 추는 동안, 4개의 색칠된 변을 지나며 새로운 색의 패턴을 만듭니다.

그렇다면 8가지 색의 패턴과 4가지 색의 패턴 사이엔 무슨 관계가 있을까요? 정답은 만약 시작과 끝이 같은 색이라면 직선이 남아있고, 아니라면 사라진다는 것입니다. 결국 오각형 위의 직선에 대하여 오각형의 표면을 변환시키는 것은 처음과 끝의 색을 변환시키는 것과 같은 작업이라는 뜻입니다.

이것이 춤으로 보여준 제 논문의 간단한 설명입니다. 만약 이 영상이 흥미롭거나 더 자세한 내용을 알고 싶으시면,  http://www. math. northwestern.edu/~diana/math/VeechPolygons.pdf 에서 직접 논문을 보실 수 있습니다.