Cutting Sequences on the Double Pentagon
film
Lisans
Emeği Geçenler
Using color and movement, this video rigorously explains what a translation surface is, and the theorem about translation surfaces that I proved in my Ph. D. thesis.
The aim of this video is to explain my Ph. D. thesis result through dance. I also have a second goal, which is to show what “math research” means (since many people think it means looking up formulas in books).
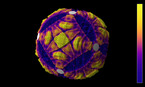
In the first minute of this video, the dancer (Libby) shows how two pentagons are glued together to make a surface. This is the key idea of the video — the explaining of science, wordlessly, through dance. You will understand it, and you will remember it. This is my favorite part!
Okay, now step back for a minute. Imagine that you are walking in a straight line on a bagel. Maybe you walk right through the hole, and return back to where you started. Maybe you walk around the outside (like an equator), and return back to where you started. Or maybe you walk in a spiraling path (still in a straight line), through the hole and around the bagel a few times before returning to where you started.
In the next part of the video, Libby dances across the pentagon in a straight line. This is exactly like your spiraling walk on the bagel: she dances in a straight line, and goes around the surface a few times (maybe 8, because there are 8 lines on the pentagons) before she returns to where she started and repeats the path.
When Libby dances across the pentagons in straight lines, she dances across the colored edges of the pentagons. We care about which ones she crosses, so we keep track of it by having a Math Hatter with that color shirt get in line. This creates a sequence of colors (which repeats with period 8).
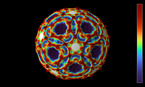
My thesis investigates what happens to this color sequence when we change the pentagon surface. We “shear, cut and reassemble the pentagons,” which is clearly shown in the video. This changes the original 8 lines on the pentagons to a different pattern — 4 lines, as it turns out. When Libby dances across these four lines, she’s doing a different, shorter spiral around the bagel (if you will). She crosses four colored edges, which gives us a new sequence of Math Hatters.
Thesis question: What is the relationship between the 8-color sequence and the 4-color sequence?
Answer: Each Math Hatter checks to see if s/he has the same color on both sides, and if so, stays in line (keeps her hat), and if not, sadly has to leave (removes his hat).
That’s my theorem: Shearing and reassembling the pentagons is equivalent to seeing if the colors are the same on both sides.
I actually wasn’t the first person to prove a theorem of this kind. John Smillie and Corinna Ulcigrai studied the regular octagon surface, which is similar to the double pentagon surface except that it is just one octagon, with opposite parallel edges identified (colored the same). They proved that if you “shear, cut and reassemble” the octagon, the effect on the color sequence is to keep only the ones with the same color on both sides. My contribution was to show that their methods also apply to the double pentagon surface.
If this interests you, it is all explained in more detail in the actual paper for which this video serves as a sort of abstract: http://www. math. northwestern.edu/~diana/math/VeechPolygons.pdf. The paper’s introduction is very friendly and has lots of pictures. In the references, you can find Smillie and Ulcigrai’s paper, whose introduction is also friendly and does a good job of explaining things. In these papers, the polygons’ edges are labeled with letters instead of colors.