Triangulating Unknown Environments using Robot Swarms
영상
저작권
크레딧
- Scientific Authors
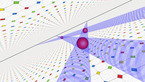
로봇의 무리가 어떻게 미지의 세계를 탐험하고 그 레이아웃을 이해할까요? 이 비디오에서는 R-one 이동형 로봇의 그룹이 이러한 임무에 이용됩니다. 로봇은 정확한 레이아웃을 찾아주지는 않는데 이는 비싼 센서가 필요하기 때문입니다. 대신 환경의 중요한 위상적 성질을 담아내는 수학적 구조인 삼각분할(triangulation)를 이용하여 대략적인 모양을 스케치합니다. 이 구조는 영역을 조사하는 다른 로봇들을 돕는 데 주는데 이용되기도 합니다. 또한 제한적인 성능을 가지는 값싼 로봇들을 이용해서도 이 구조를 만들 수도 있습니다.
최근 로봇 공학의 경향은 두 가지로 나뉩니다. 하나는 최신식 기계를 상대적으로 높여 로봇 각각의 성능을 향상해 프로세스를 이해하는 것이고 다른 하나는 로봇의 성능을 희생하는 대신 더 단순하고 값싼 플랫폼을 개발하는 것입니다. 후자는 제한된 성능을 가진 많은 로봇을 탐험, 감시 안내 등의 어려운 임무들을 수행하는 집단이 되도록 조직화하는 것 등 새로운 원리나 알고리즘을 개발해야 한다는 어려움을 남깁니다.
이 영상은 로봇 무리에 관련된 이론과 실제 작동에 관한 공동작업을 보여줍니다. 우리는 어떤 영역을 조사하고 탐험하는 제한된 소통 범위를 갖는 로봇 무리에 관련된 문제를 고려합니다. 최소 연결 삼각분할 문제(minimum relay triangulation problem, MRTP)는 로봇의 소통 그래프가 주어진 영역을 삼각분할하는 최소한의 로봇의 개수를 찾고자 합니다. 최대 면적 삼각분할 문제(maximum area triangulation problem, MATP)는 소통 그래프가 뿌리(root)를 포함하고 가능한 가장 큰 면적을 덮는 삼각분할을 만드는 n개의 로봇의 위치를 찾고자 합니다. 또한 실제 R-one 플랫폼에 어떻게 이용되는지 보임으로써 방법론들의 타당성을 보여주고자 합니다.
이 비디오는 29회 계산기하 심포지엄(Annual Symposium on Computational Geometry)에 있었던 22회 계산기하 비디오/멀티미디어 회고(Annual Video and Multimedia Review of Computational Geometry)에 속합니다.