MathLapse- L- System for Single Knot Kolam Pattern Generation II
영상
저작권
크레딧
- Design and Development
Lindermayer system is a parallel rewriting system and a type of formal grammar. It consists of an alphabet of symbols that can be used to make strings, a collection of production rules that expand each symbol into some larger string of symbols.
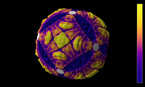
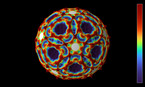
The recursive nature of L system rules leads to self similarity and thereby fractal like forms are easy to describe with an L system. This nature is applied in generating kolam pattern. Kolam pattern becomes more complex by increasing the iteration level.
Software: Python Turtle Graphics
SUZHI / KAMBI / SIKKU Kolam
In the art form of SUZHI KOLAM/ KAMBI KOLAM, dots called pulli are arranged in rhombic, square, triangular, or free shapes, and a single, uninterrupted linear or curvilinear line, called the kambi, intertwines the dots. While there are no written or verbally stated rules. Listed some rules of pulli(dots) and kambi/Suzhi kolam from examining the designs (Yanagisawa, Nagata, Robinson Thamburaj). Rules can be added / removed.
Rule 1: Uniformly spacing of dots
Rule 2: Smooth drawing line around the dots
Rule 3: Symmetry in drawings
Rule 4: Straight lines are drawn inclined at an angle of 45 degrees
Rule 5: Drawing lines never trace back
Rule 6: Arcs adjoining the dots
Rule 7 : Kolam is completed when all points are enclosed by the drawing line
Kolam drawing can be treated as a special kind of a graph with the crossings considered as vertices and the parts of the kambi between vertices treated as edges. The only restriction is that unlike in a graph, these edges cannot be freely drawn as there is a specific way of drawing the kolam. The single kambi kolam will then be an Eulerian graph with the drawing starting and ending in the same vertex and passing through every edge of the graph only once. Single knot kolam also called as “ANTHATHI Kolam” in Tamil Nadu. The Smooth line starts at a point and end in the same point. Single knot kolam can be drawn for any type of dot structure (rhombic, square, triangular, or free shapes).
L-System
Lindermayer system is a parallel rewriting system and a type of formal grammar. It consists of an alphabet of symbols that can be used to make strings, a collection of production rules that expand each symbol into some larger string of symbols.
The recursive nature of L system rules leads to self similarity and thereby fractal like forms are easy to describe with an L system. This nature is applied in generating kolam pattern. Kolam pattern becomes more complex by increasing the iteration level.
Software: Python Turtle Graphics
Applying L-System for Kolam pattern Generation:
Procedure:
Axiom or Initiator: FBFBFBFB
Rules: A —>AFBFA
B—>AFBFBFBFA
From current cursor position ,
F à Forward 10 units (draw a line 10 units length)
A à Draw an arc (circle (10, 90))
B à Calculate forward units I = 5/sqrt (2)
Forward I Units
Draw an arc (circle (I, 270))
Forward I Units
Execution:
0TH Iteration : FBFBFBFB// Initiator
1ST Iteration : F AFBFBFBFAF AFBFBFBFAF AFBFBFBFAF AFBFBFBFA
//apply the ruleB—>AFBFBFBFA
2ND Iteration : FAFBFA FAFBFBFBFA FAFBFBFBFA FAFBFBFBFA FAFBFA
FAFBFA FAFBFBFBFA FAFBFBFBFA FAFBFBFBFA FAFBFA
FAFBFA FAFBFBFBFA FAFBFBFBFA FAFBFBFBFA FAFBFA
FAFBFA FAFBFBFBFA FAFBFBFBFA FAFBFBFBFA FAFBFA
//apply the rule A —>AFBFA B—>AFBFBFBFA
and so on…