Energy flux of waves with dodecahedral symmetry on the sphere
영상
저작권
크레딧
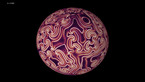
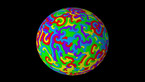
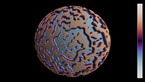
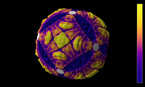
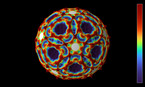
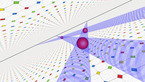
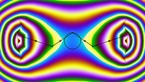
Solution of the wave equation on a sphere. Reflecting obstacles have been placed around the vertices of a regular dodecahedron. The initial state is a set of circular waves concentrated at the centers of the faces of the dodecahedron. The colors and radial coordinate represent the energy flux.
The simulation shows a solution of the wave equation on a sphere, obtained by a finite difference scheme. There are Dirichlet boundary conditions on a set of discs of constant radius placed on the vertices of a regular dodecahedron. The initial state is a set of circular waves concentrated near the centers of the faces of the dodecahedron, which form a regular icosahedron.
The point of view rotates around the sphere in the course of the simulation. In both parts, the radial coordinate and luminosity show the norm of the energy flux, while the color hue depends on its direction. Two different color gradients are used (Jet in part 1, twilight in part 2).